
Is there a way to avoid all that extra dough in between the cookies? (Photo: Christmas Tree Cookie Cutter from Bigstock)
It should come as no surprise that food, chemistry and mathematics meet in baking. For once I will leave the chemistry aside for a while and turn to the mathematical aspects of baking. More precisely I will delve into geometrical problems encountered in baking. When cutting cookies from a rolled out dough or placing cookies on a sheet for baking you actually attempt to solve a mathematical problem known as a packing problem. The purpose is to maximize the distance between the cookies and maximize the size of the cookies, paying attention that the cookies should not touch. Many will perhaps start with a square packing (see below), but soon figure out that a hexagonal packing will fit even more cookies onto the rolled out dough or onto the baking sheet (especially when the dough/sheet is large compared to the cookies). The optimum way of placing 2-17 circles in a square are shown below (and the solution for up to 10.000 circles is also available).
My challenge for you however is a different one as I’m interested in eliminating the leftover dough when cutting cookies. To achieve this the cookies cannot be circular. Using a square cookie cutter (or simply a knife) would be the easiest way to leave no gaps, but how cool are square cookies? What I’m really looking for are cookie tessellations which are aesthetically pleasing, and at the same time transferable to a baking sheet. Oh yeah: a tessellation “is the process of creating a two-dimensional plane using the repetition of a geometric shape with no overlaps and no gap” according to Wikipedia. So – no gaps – no leftover cookie dough!
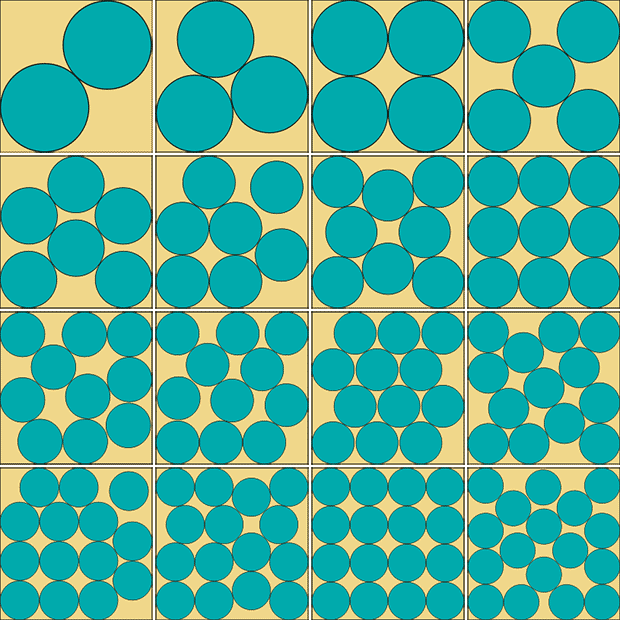
Should you ever want to place circular cookies on a square baking sheet, this is how to maximize the size of the cookies! (Illustrations CC-BY-SA by Toby Hudson)
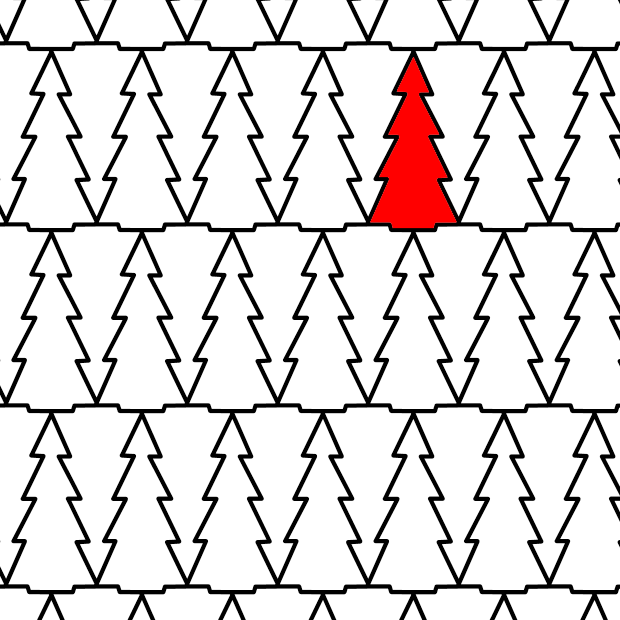
This is one way of solving the problem with leftover dough shown in the top picture. A tree can quite easily be transformed into a shape that fills the plane without any gaps. This image was made using the Tess software mentioned below.
Tessellations are frequently encountered in the art of M. C. Escher, and his Regular Division of the Plane Drawings are all based on tessellations. Most of Escher’s drawings however are not useful for making cookies because they are too interlocking – it would be impossible to take the cookies apart and transfer them to the baking sheet (and baking them “interlocked” would not be an option as cookie dough inevitably will raise/expand a little, making everything stick together). But I did find one example of an Escher inspired cookie cutter as well as some other nice examples of cookie cutters especially designed to make tessellations:

Over at Thingiverse the design file for this Escher inspired cookie cutter can be downloaded (Photo by Bas Pijls via Thingiverse). And should you want to transfer your own designs into a 3D printable format, check out this cookie-cutter-generator.

From Cox & Cox you can buy this Jigsaw cookie cutter (Photo from Cox & Cox product page). If you have access to a 3D printer you can also print your own jigsaw cookie cutter.

These elaborate cookie cutters are designed by Keith Kritselis. Over at Kickstarter you can find more information about his special cookie cutters for Halloween and Christmas. What makes them special is that each tessellation is made up of three or four different shapes.
If you rather want to make your own tessellations there are a couple of different software and online apps available, but I’ve found Tess to be one of the best. An evaluation copy of Tess (no save function) can be downloaded for free. Below are a couple of designs I’ve made. The patterns are nice, but would I want to each cookies with these shapes?
And finally the challenge for you all: Make your own cookie tessellations and share it! It’s not a competition, but rather an invitation to contribute. If the design is great I might have it 3D printed on a friends MakerBot or order it in metal from Shapeways and blog about it here 🙂 If you send pictures to me at hello@khymos.org I can put up a gallery to display the submitted designs.
Further reading: Merry Christmas to all geeks

I would pay a lot for some Penrose/quasicrystal cookie cutters! Shouldn’t be too hard if they’re just the kite/dart combo.
I’ve made tangram gingerbread for friends before. It’s good for posting to people as a gift.
I think the dough tastes better than the cookies themselves so I don’t see any “problem”. 🙂
[…] Se her: http://blog.khymos.org/2012/01/19/recreational-kitchen-mathematics-cookie-tessellations/ […]
The cutter should be made into a roller to make for less waste, like a rolling pin that has the pattern inlaid.
Excellent article, thank you! I used to have a cookie cutter rolling pin. It was awesome. Wish someone would market that again. …Susan
You mean something like this gingerbread cookie roller?
I am so glad you posted this. I have been trying to convince my Pastry Chef that these are a good idea. We designed them in grade 5 math class, as a fun excersise.
“Heesch tilings” is a good search term for more ideas—love the Penrose kite/dart idea.
https://faculty.washington.edu/cemann/Heesch.pdf